5 Compounding Rules and How much is a Penny doubled for 30 days

"My wealth has come from combination of living in America, some luck genes and compound interest" - Warren Buffett

Compounding works best when starting young

---

Table of Contents

1. Executive Summary
2. 1 Penny vs 1 Million dollars
3. Compounding in the stock market
4. Indian Legend about the rice farmer

---

Executive Summary

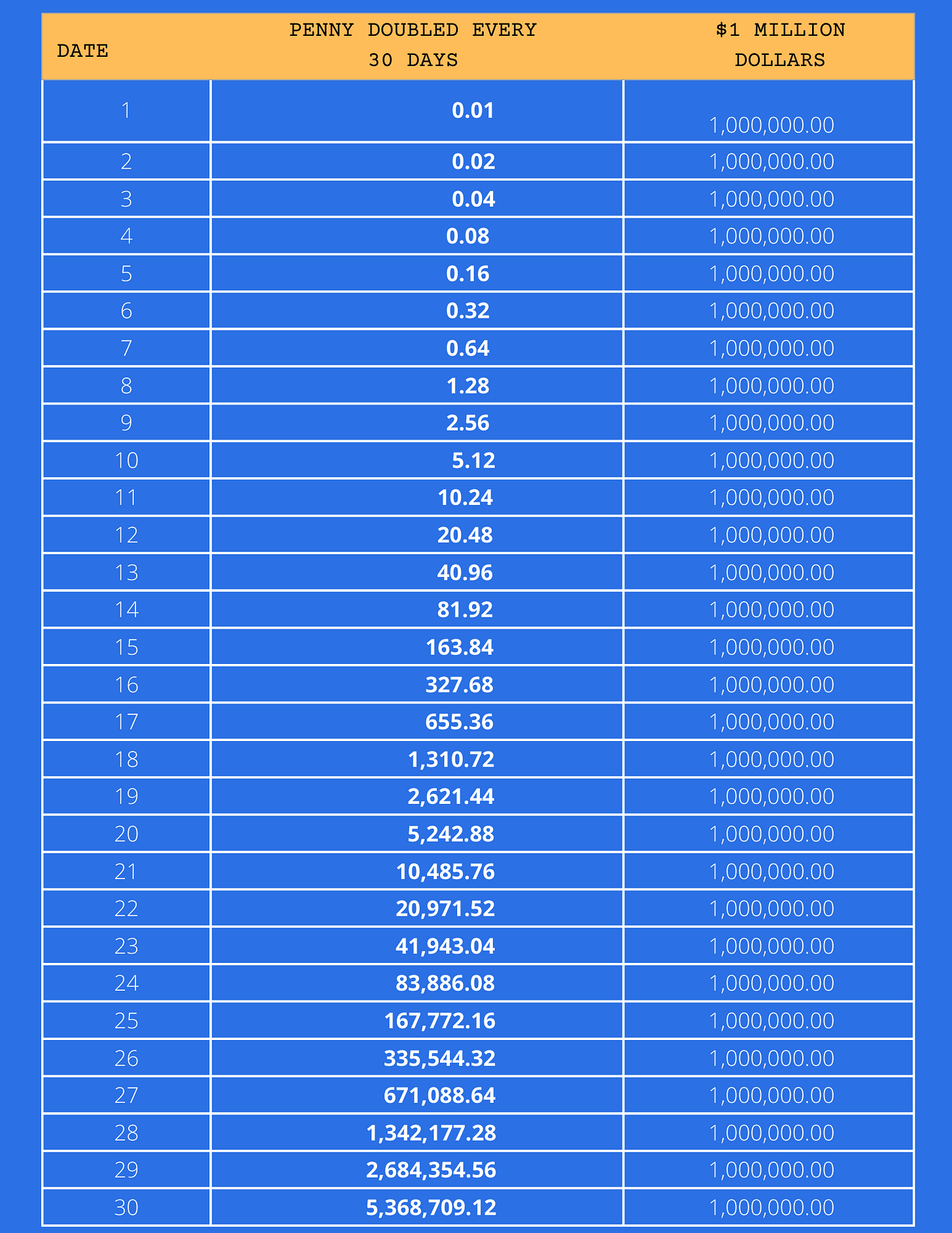
• 1 Penny doubling for 30 days results in $5,368,709.12

• After 27 days the doubling penny brings more than $1 million

• Compounding Rule 1: Losses are asymmetric

• Compounding Rule 2: Limiting losses stop negative compounding

• Compounding Rule 3: Road to over 100% returns needs only 37 stock picks

• Compounding Rule 4: Compounding allows you to be progressively more conservative

• Compounding Rule 5: Better results can be achieved faster when you deploy compounding

• Compounding effect = the more you make the easier it is to make more

---

1 Penny vs 1 Million dollars

The magic penny riddle is something that I discovered when I was a kid. It goes something like this:

"Would you rather have a penny doubled for 30 days or $1 million dollars?"

Of course my primal instinct, did some basic calculations and I was sure that a penny doubled for 30 days cannot be, in anyway, more than million bucks. I was quick to go for the $1 million dollars answer, but my maths teacher soon explained that a penny doubled for 30 days is more than a million dollars. Of course, to my surprise this was the beginning of my fascination of compound growth and the base for my understanding of why you ought to start investing early. Turns out that a penny doubled everyday for 30 days actually brings a huge amount of money. $5,36,09.12 to be exact. Even today it still seems strange but the power of compounding has been a fascination of many of our great minds. To quote Albert Einstein:

"Compound interests the eighth wonder of the world"

Whether you choose a penny doubled for 30 days or a million dollars, the key takeaway is that money making more money is the secret to grow wealth.

1 penny vs 1 million dollars compounded daily

Here is the data for the graph above, as you see after day 27, the penny doubled for 30 days starts making exponential advancements achieving its status as the "magical penny".

1 penny vs 1 million dollars in a table form

---

Compounding in trading the stock market

In this section, I want to review the ways compounding finds its way in trading, and why I believe it is important for you to pay attention to it. I have structured the key takeaways in the form of 5 Rules to bring edge in your trading.

Rule #1: Compounding hits both losses and winners

One of the core principles for trading is that there is the phenomenon of asymmetric losses. Those who do not understand the nature of asymmetric losses are deemed to suffer sooner or later ruin in the markets.

Just like the penny doubled for 30 days, as you see below, small amounts mount up. In the case of the stock market, small losses require exponential gain to get back to break even. In other words it becomes exponentially more difficult to break-even the initial investment.

Asymmetric losses in trading and required gain to break-even

This is even more exaggerated when you start looking at consecutive losses. In other words we can see that 2 consecutive losses of -10% would require 23% gain to get back to breakeven and 3 consecutive losses of -10% would require 37%. The graph below looks only at losses of max size of -55% and we see that the exponential break-even requirement compounds a lot when we have consecutive losses.

Asymmetric losses in 2 consecutive losses nad 3 consecutive losses

Here is a table of the above graph. As you see loss size of over 20% makes it extremely difficult to be made up especially if we look at 3 consecutive losses of this kind and not to forget the chance of 3 consecutive losses is over 96% if your long term batting average is less than +60%! My personal long term average is losses of -6% and in difficult times (like 2022), I average losses of -4%.

Asymmetric losses in table form and required gain to break-even

Key takeaway: Losses work asymmetrically against traders

Rule #2 Limiting losses makes wonders

In the below example, I take 2 traders - Alice (no loss limiting trader) and Bob (loss limiting trader). Both Alice and Bob, make 20 trades and in those 20 trades make exactly the same winners, averaging 18.30%. Both have the same batting average of 50% and both trade the same equities no margin. The only difference is that Alice is sloppy on cutting losses, whereas Bob is strict and does not let anything slip under -10% bar. In fact, the average loss for Alice is -15.55% and for Bob is -10.00%. Can you guess what is the Annual PL for both?

Here is the answer:

Alice: -1%

Bob: +78%

Now this is huge by any standard. The main point here is that you are going to have losses and as per Rule #1 they will work against you. Keeping those losses small is your ONLY real protection against large losses. Rule #1 showed us that it is difficult to make a case for keeping losses more than -10%. So chose what level is right for you, but stress test it mathematically, just to make sure you have achieve a penny doubled result and not a mistake compounded result.

Alice: non loss limiting trader result in table form

Bob: Loss limiting trader result in table form

Key takeaway: Limiting losses can stop negative compounding.

Rule #3 Road to +100% return

Now the third eye-opening principle of compounding is how little it takes to reach your goal when you use compound interest! Let's suppose as a trader your goal is triple digit return, in other words +100%. We know we have 253 days in a year (alternatively you can use the example with 253 trades). For an achievable assumption we are going to use 2% gain on the account value. If this seems a lot, it is the same as saying an 8% gain on a 25% position. So to show you how magically the numbers works, just like the penny doubling, keep on reading.

If we assume that for 85% of the trading days you are cash or breakeven. Do you know how many stock picks you need for the year in order to achieve +100%? Only 37, with 25% exposure and 8% gain on them. Doesn't sound like a lot right? That's about 9 stocks per quarter, which is very easily achievable. The secret of course is to not have the large losses (Rule #2).

Now if you still think this is much we can decrease the target to 70% or 40% return per year. In this case you will need only 27 and 17 stock picks per year that go up 8% and the rest of the time you can be in cash. This is as between 4-6 stocks per quarter! Notice, we are not talking about the next Amazon or Apple, we are talking about advancement of 8% and nothing else. 

The magic of course comes from compounding interest just like it did for the penny doubled for 30 days. You can see in the picture below, how little it takes to be right (cyan box).

Road to +100% return with market participation time

Key takeaway: To make over 100% return in a year I need to find only 37 stock.

Rule #4 Compounding allows you to be progressively more conservative

The idea to this rule is to show you how you can get progressively more conservative. It shows that once you get up big (+30%) in 1 quarter, you can tighten parameters and do not have to be fully invested in order to make the target of triple digit return.

As we saw in the penny doubled for 30 days, each dollar that you make is going to earn interest in the next step and this is the road to double your money. This means that to achieve triple digit next quarter you only need +20%, and the following quarter only +15% and the last quarter only +10%.

In essence if we can make +30% on each quarter, the compounding factor would mean that in quarter 4 we will be making 2.2 times more on every earned dollar.

However, a word of caution - as we saw in Rule #1 - compound interest works both ways and just as easily a novice trader can compound mistakes rather than winner!

Compounding gains in 100k account makes it easier as you make results. Orange is PL % gain, Cyan is theo account size

Key takeaway: Compounding interest means you can get more conservative

Rule #5 Trading Opportunities and Gain goals

The last rule uses an economic term of opportunity cost. I got thinking about this after a friend (non-trader) posed this trick question while I was explaining to him the concept of True Market Leaders. "TinTin, why are people looking for this infrequent winners when they can buy stocks that advance small amount and compound interest on that?"

It got me thinking because it is definitely easier to find 8 stocks that make 10% move (compounded to 114%) than the next Tesla that makes +100%. Apart from easier, smaller moves are also faster, meaning that you can get to your goal faster. Just like the trick question about do you want a penny doubled for 30 days or a million dollars today.

You might have seen this picture from Mark Minervini's book. It shows that when you adjust the % gain for the number of days it takes (in other words how frequent this opportunity will be in a trading year) the most lucrative gain segments fall under 25%. This also coincides well with the 20-25% average gain that William O'Neil talks before the throwback phenomenon (link to article on the subject here).

Trading opportunities per gain bracket

Key takeaway: By taking compound interest we see that gains up to 25% allow for the best trading results

---

Indian Rice Fable: Rice Farmer outsmarts the Emperor

I started with a story and I want to finish with a legend. The legend about the Farmer, Emperor and the Chess Board alludes to the fable surrounding the creator of the game of chess.

According to legend, when a great monarch received chess, he promised the creator any gift he desired. The creator requested that one rice grain be placed on the chessboard's first square. Then two grains on the following square and four grains on the subsequent square. Doubling every time. The monarch instantly consented and gave the treasurer the order to pay the agreed-upon amount after being confused by such a low payment for such an amazing game.

The inventor went before the king a week later to inquire as to why he had not yet received his award. The king summoned the treasurer right away and demanded to know why the inventor hadn't been paid and was furious that the treasurer had defied him. The treasurer stumbled and explained that when he went even halfway through the chessboard, the amount of grain needed to cover the balance was more rice than the entire kingdom had, therefore the amount could not be paid.

The main purpose of this fable is to teach us about the importance of exponential growth and compounding. There is only one grain of rice on the first square of the chessboard, but as you move down the board, the number grows until you reach square 64, where there are nearly 18 quintillion grains of rice. The legend serves as another illustration of extraordinary growth in mathematics.

---

Thank you!

💡These posts consume most of my Sundays! If you have received value:

• Share it on Twitter (using the button below)

• Subscribe to the newsletter.

This way You will help grow the community together!